
© François Le Coat
©Karl Samyn
Last modified :
July 6 2012
|
\ ----------------------- / >>>> EUREKA 2.12 02/87 <<<< / ----------------------- \ brève description Note : See registering conditions following hereafter. Installation : Copiez TOOLS\RECORD.ACC & SCR_DMP.ACC sur C. Si vous avez GEMVIEW, copiez GEMVIEW.MOD\ICN.GVS dans le dossier GVWSAVE et GEMVIEW.MOD\EURAW.GVL dans GVWLOAD. Rien de plus ... Eurêka est un traceur. Il permet de visualiser des graphes de fonctions mathématiques diverses définies dans "HELP". Il est possible de proposer des expressions élaborées qui seront analysées grâce à un évaluateur d'expressions. Il est possible de définir des expressions à valeur complexe puisque la constante symbolique i telle que i*i=-1 est présente. Avant de tracer ( menu Courbe->Tracer ) une courbe il est nécessaire de définir le système dans lequel celle-ci va être tracée. 1) Le menu système Le menu système se divise en deux parties.
On peut définir des graphes dans le plan ou dans l'espace. Le plan
possède deux dimensions, tous les graphes dans le plan seront tracés
en laissant varier une variable. L'espace possède trois dimensions,
tous les graphes dans l'espace seront tracés en laissant varier
deux variables.
1.1) Dans le plan Les limites dans lesquelles la variable se situe sont définies conjointement à la définition du système, au moment du tracé ( menu Courbe->Tracer ). Cela dépend du système choisi. Les axes sont orthogonaux de plus le système peut être orthonormé en choisissant l'option "NORMER" ( de la fenêtre proposée après Système->Cartésien ou Système->Polaire ). 1.1.1) Cartésien Le plan cartésien est défini par ses limites en abscisse ( x ) et en ordonnée ( y ). Les limites du plan peuvent être arbitrairement élevées. Il faut toutefois se borner à un choix qui est décidé par les critères suivants : 1.1.1.1) Cartésien - Analytique Le graphe a une forme analytique y=f(x). Les limites proposées en abscisse ( x ) vont donc déterminer l'intervalle de variations de la fonction f. De la même façon les limites en ordonnée ( y ) ne seront bien choisies, que si elles correspondent à un intervalle significatif pour les variations de la fonction y=f(x). Par exemple : y=sin(x) ; un intervalle intéressant pour observer y est l'intervalle
suivant :
Il est aussi possible en mode Cartésien -
Analytique de dériver ou intégrer numériquement une
expression y=f(x). Il faut alors au moment de tracer la fonction revenir
dans le menu Système->Cartésien->flèche en ayant décidé
laquelle des 3 courbes de A à C sera f(x) et placer la dérivée
f'(x) ou l'intégrale F(x) dans les 3 courbes de D à F. On peut pour
l'intégrale ajouter une constante à celle-ci qui corresponde
par exemple à F(INF(x)) ou à 0. Pour cela on peut donner
une expression élaborée de la forme g(x) où x représente
la limite inférieure INF(x) donnée en abscisse dans le menu
système. Par exemple pour f(x)=sin(x) que l'on désire intégrer,
la constante à ajouter à l'intégrale pourra être F(INF(x))=-cos(x).
Dans le cas général où on ne connaît pas l'expression
formelle de F(x), on choisira une constante nulle. De cette manière
l'intégrale calculée sera la suivante :
1.1.1.2) Cartésien - Paramétrée Le graphe a une forme paramétrée :
1.1.2) Polaire Le système de coordonnées polaires
est défini en abscisse ( x ) et en ordonnée ( y ) par la définition
d'un angle t par rapport au segment (Ox) O étant l'origine (0,0)
et x représentant l'axe des x, et d'une distance r du point (x,y)
par rapport à l'origine. On définit les coordonnées
polaires par le système suivant :
1.1.2.1) Polaire - Analytique Le graphe est déterminé par la fonction
r=R(t). Pour apprécier les limites en abscisse ( x ) et en ordonnée
( y ), il faut préalablement connaître quel sera le domaine
de variations de R(t) en fonction du domaine de variations de t. Par exemple
pour la spirale d'Archimède définie par :
1.1.2.2) Polaire - Paramétrée Le graphe est déterminé par le système d'équations
paramétrées :
Il faut remarquer que les coordonnées Polaires - Analytiques ne sont autres que les coordonnées Polaires - Paramétrées en posant THETA(t)=t. 1.1.3) Image 2D Le système de coordonnées image 2D permet de tracer une surface c=P(x,y). c est un niveau dans le système de couleurs de l'ordinateur et x & y sont les axes horizontaux et verticaux respectivement. c varie donc entre 0 et le nombre de couleurs affichables par l'ordinateur. Si c ne se trouve pas dans l'intervalle, il est réduit modulo le nombre de couleurs affichables. 1.2) Dans l'espace Dans les systèmes de coordonnées de l'espace, il est possible de représenter une surface dépendant de deux variables. Les axes de coordonnées forment un repère direct tel que : 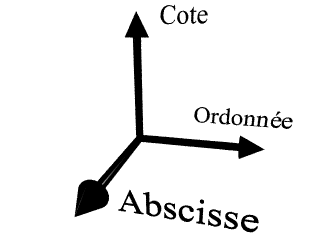 Les surfaces représentables sont de la forme Z=f(x,y). Il suffit de définir l'intervalle de variations des variables x et y, et les limites du tracé de Z. 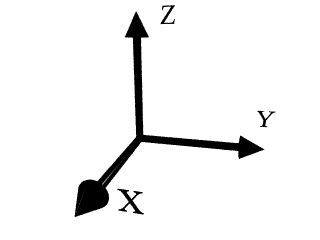 en abscisse : -10 10__________________________________ en ordonnée : -10 10__________________________________ en cote : -1 1____________________________________ La surface A sera obtenue en donnant la fonction Z(x,y)= sin(r)/r________________________________ dans ce cas r=sqrt(x^2+y^2). De même on peut utiliser la variable t telle que : t=atg(y/x). 1.2.2) Coordonnées cylindriques Dans ce système de coordonnées il est possible de représenter des surfaces s=F(r,t,z). Les coordonnées sont définies par : 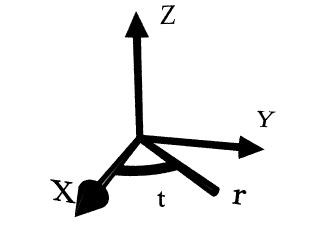 thêta : 0 2*PI__________________________________ z : -1 1____________________________________ Les limites de l'espace seront alors : en abscisse : -2 2____________________________________ en ordonnée : -2 2____________________________________ en cote : -2 2____________________________________ La surface cylindrique sera obtenue en donnant la fonction Fr(r,t,z)= 1_______________________________________ Ft(r,t,z)= t_______________________________________ Fz(r,t,z)= z_______________________________________ 1.2.3) Coordonnées sphériques Dans ce système de coordonnées il est possible de représenter des surfaces s=F(r,t,p). Les coordonnées sont définies par : 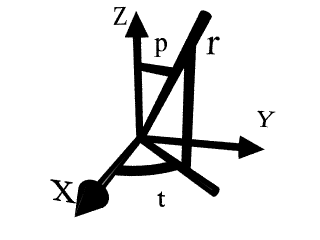 { x=r*sin(p)*cos(t) { y=r*sin(p)*sin(t) { z=r*cos(p) Pour tracer une courbe on choisit l'intervalle de variations de r t et p, sachant que l'une des trois restera constante (une surface dépend de deux variables). On donnera ensuite les limites de l'espace. Pour tracer une sphère on pourra définir r constant et thêta : 0 2*PI__________________________________ phi : 0 PI____________________________________ Les limites de l'espace seront alors : en abscisse : -2 2____________________________________ en ordonnée : -2 2____________________________________ en cote : -2 2____________________________________ La surface sphérique sera obtenue en donnant la fonction Fr(r,t,p)= 1.5_____________________________________ Ft(r,t,p)= t_______________________________________ Fp(r,t,p)= p_______________________________________ 1.2.4) Paramétré 3D Il existe deux systèmes de coordonnées paramétrées. Dans les deux cas deux paramètres varient. Ils peuvent être soit x et y ; c'est le système rectangulaire, soit r et t (ou u) ; c'est le système polaire. 1.2.4.1) Rectangulaire Dans ce cas :
Dans ce cas :
ADDENDUM 1 - Ensemble des fonctions utilisables "asinh" ex : asinh(x) "acosh" ex : acosh(x) "atgh" ex : atgh(x) "abs" ex : abs(x) "ash" ex : ash(x) "ach" ex : ach(x) "ath" ex : ath(x) "atanh" ex : atanh(x) "acos" ex : acos(x) "asin" ex : asin(x) "atg" ex : atg(x) "atan" ex : atan(x) "arg" ex : arg(x+i*y) "cos" ex : cos(x) "ch" ex : ch(x) "coth" ex : coth(x) "cotanh" ex : cotanh(x) "cotg" ex : cotg(x) "cotan" ex : cotan(x) "conj" ex : conj(x+i*y) "ceil" ex : ceil(x) "data" ex : dataa(x) "dftd" ex : dftda(x) "dfti" ex : dftia(x) "degrees" ex : degrees(Pi/2.0) "exp" ex : exp(x) "ent" ex : ent(x) "err" ex : err(x) "fac" ex : fac(x) "floor" ex : floor(x) "fit" ex : fita(x) "fftd" ex : fftda(x) "ffti" ex : fftia(x) "gamma" ex : gamma(x) "hside" ex : hside(x) "int" ex : int(x) "im" ex : im(x+i*y) "inf" ex : inf(x,y) "julia" ex : julia(x+i*y,x+i*y) "j'" ex : j'(x,y) "j" ex : j(x,y) "ln" ex : ln(x) "log" ex : log(x) "line" ex : linea(x) "max" ex : max(x,y) "min" ex : min(x,y) "mod" ex : mod(x,y) "p10" ex : p10(x) "pow" ex : pow(x,y) "poly" ex : polya(x) "psd" ex : psda(x) "peak" ex : peaka(10,x) "rand" ex : rand(1000.0) "radians" ex : radians(10.0) "rect" ex : rect(x) "re" ex : re(x+i*y) "sin" ex : sin(x) "sqrt" ex : sqrt(x) "sh" ex : sh(x) "sgn" ex : sgn(x) "sup" ex : sup(x,y) "samp" ex : sampa(x) "smooth" ex : smootha(x) "spline" ex : splinea(x) "surf" ex : surfax(x,y) "th" ex : th(x) "tanh" ex : tanh(x) "tg" ex : tg(x) "tan" ex : tan(x) "wville" ex : wvillea(x,y) 2 - Ensemble des options utilisables (après un ";") "iter=" ex : ;iter=256 "angle=" ex : ;angle=180 "!rotate" "!flip" "!logx" "!logy" "!norm" "!gridmax" "!gridmay" "!gridmix" "!gridmiy" "!gradmax" "!gradmay" "!gradmix" "!gradmiy" "rotate" "flip" "color=" ex : ;color=image "sub=" ex : ;sub=5 "majgx=" ex : ;majgx=8 "mingx=" ex : ;mingx=10 "majgy=" ex : ;majgy=6 "mingy=" ex : ;mingy=10 "mesh=" ex : ;mesh=101*51 "cmap=" ex : ;cmap=hot.map "ccmap=" ex : ;ccmap=jet.map "solid" "logx" "logy" "norm" "black" "noir" "white" "blanc" "gridmax" "gridmay" "gridmix" "gridmiy" "gradmax" "gradmay" "gradmix" "gradmiy" "mem" ex : ;mem12=10.0 3 - Ensemble des constantes utilisables "mem" ex : mem12 "i","I" ex : cos(x)+i*sin(y) "pi","PI","Pi" ex : Pi/2.0 "eu","EU","Eu" ex : pow(Eu,x) "m" ex : m0 "du" ex : dua "fr" ex : fra "xmin" ex : xmina "xmax" ex : xmaxa "ymin" ex : ymina "ymax" ex : ymaxa "time","clock" Ce programme est un free-shareware-ware. C'est à dire que tout auteur de shareware utilisant ce programme, s'engage à m'envoyer celui-ci en me faisant grâce de sa contribution. J'espère ainsi d'une part avoir une bibliothèque de logiciels intéressants, et d'autre part, tenir compte du développement de chacun pour rendre mes productions interfaçables avec les vôtres. Les auteurs de freewares sont aussi vivement encouragés à me faire parvenir leurs productions. Pour les personnes qui ne sont pas développeurs, vous pouvez m'aider dans mes efforts en m'envoyant 15 Euros. Il est strictement interdit de modifier ce programme ou d'en utiliser des parties sans mon autorisation. Vous n'avez pas le droit d'enlever des fichiers de l'archive. Vous devez la transmettre Intégralement et Gratuitement. Certains organismes auront le droit de demander des frais de copie et uniquement de copie, du moment qu'aucun bénéfice n'est fait sur mon dos ... J'autorise les magazines à mettre ce programme
sur leur disquette/CDROM à condition qu'ils m'envoient gratuitement le
numéro correspondant, ce qui n'est pas trop demander je pense.
This software is a free-shareware-ware. It means that any shareware author that
uses this program, shall send me his proper software without asking the contribution
fees. I wish to have a good software library, but furthermore I will manage to improve
usage compatibility with your own software. Freeware authors are also concerned, and
should send me their production. For non authors, they may send me fees equivalent
to 15 Euros.
It is strictly forbidden to modify this software, or use parts of it without
my agreement.
You must not extract parts of this archive. You must diffuse the whole archive
with no fees. Some institutions would require an amount of copy fees, and strictly
for copying, so far as no profit is made out of my work.
Magazines can distribute the program, so far as they send me a free copy of it.
I think that it is not a too demanding condition.
This program is supplied with no guarantee of any kind. You use
it at your own risks. No complain can be made on miss use of it, or what
so ever. |
|||